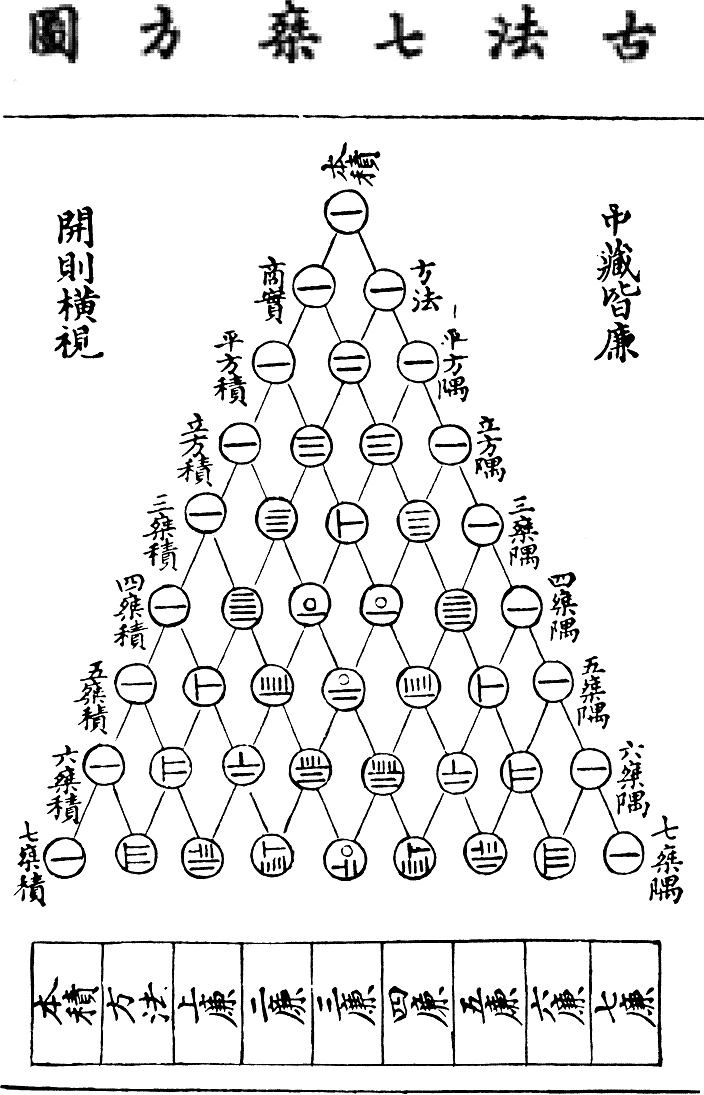
Sistemas de numeración
A continuación se presentan números en diferentes sistemas de numeración. Puede intentar deducir el valor de cada signo, posteriormente se expondrán algunas deducciones.
| Sistema numeral | ejemplos | ejs. claves | ||
|---|---|---|---|---|
| egipcio | 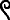 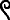 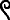 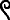 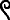 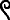 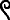 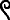        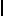 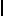 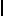 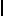 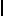 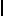 |
876 | ||
| ático | 𐅅ΗΗΗ𐅄ΔΔΔΠΙΙΙ | 888 | 𐅄𐅅𐅆𐅇 | 5555 |
| etrusco | 𐌣𐌢𐌢𐌢𐌡𐌠𐌠𐌠 | 88 | 𐌣𐌢𐌢𐌢𐌢𐌡𐌠𐌠𐌠𐌠 | 99 |
| romano | LXXXVIII | 88 | XCIX | 99 |
| chuvash | II/  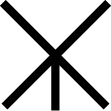    
|
876 | I/    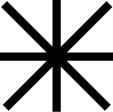 |
1666 |
| griego (y derivados) | ΗΠΩ | 888 | ΑΙΡ | 111 |
| brahmi | 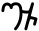   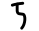 |
888 | 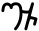  
|
555 |
| árabe | غضفح | 1888 | ضفحغ | 888000 |
| sabeano, minaeano¹ | 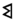 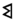     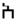 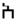 |
282000 | 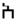 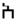 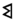 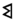     |
2280 |
| chino (también japonés) | 八百八十八 | 888 | 一十二萬三十 | 120030 |
| hindú | ८८८ | 888 | १००० | 1000 |
| 籌 (numeración con varillas) |  |
1955119680 |  |
327 |
| babilónico |  |
59 o 3540 o... |  |
1 o 60 o... |
| maya |   |
88 | 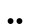  |
42 |
¹ se ha forzado el orden, que originalmente es de derecha a izquierda, para facilitar la comprensión.
La mayor dificultad en la deducción de los ejemplos presentados proviene del uso de bases distintas a 10, de
la
combinación de potencias y unidades o de cómo la sucesión de cifras determina la operación aritmética. El
siguiente ejemplo de la escritura karosti es complicado por sus irregularidades y
representa el
número 1996
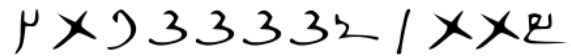
Deducciones y detalles
Se pueden concluir cinco categorías:
primera categoría. Egipcio
El egipcio es el sistema más arcaico como se deduce por el grado en que se apoya en la repetición: es puramente aditivo y sin base auxiliar. Sin embargo resulta más conveniente para el cálculo que las dos siguientes categorías.
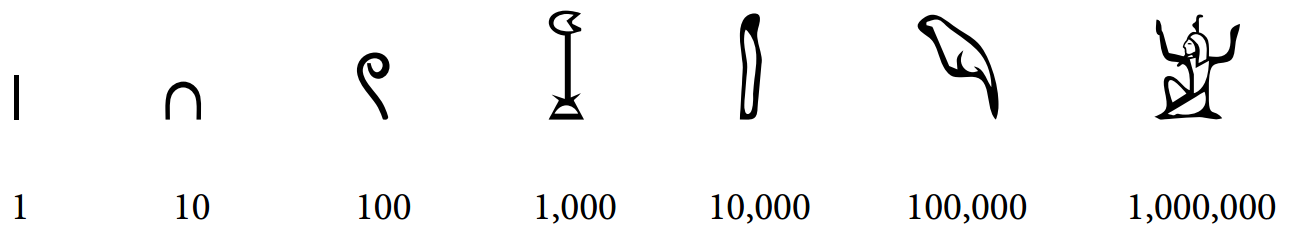
segunda categoría
El ático, etrusco, romano y chuvash son similares. Podemos observar una secuencia de 3+1 elementos como en
los
grupos 𐅅ΗΗΗ, 𐅄ΔΔΔ y ΠΙΙΙ del ático 𐅅ΗΗΗ𐅄ΔΔΔΠΙΙΙ para
expresar la cifra 8. Esto implica que existe una base auxiliar gráfica para reducir la repetición de
elementos:
la base es 10 y la sub-base es 5. Así en vez de tener que expresar como en egipcio:
9 = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1, tenemos:
9 = 5 + 1 + 1 + 1 + 1
El ático ΙΠΔΗΧΜ (posiblemente del s. VII AEC) es el sistema numérico más
interesante de esta categoría. Es el más coherente por varias razones: es puramente aditivo; la sub-base 5
Π se compone gráficamente siguiendo un principio multiplicativo con las
potencias
Δ Η Χ Μ dando lugar a 𐅄 50, 𐅅 500... Además es
acronímico, esto es, establece el signo según el de la primera letra de la palabra que los
nombra:
| Ι | Π | Δ | Ε | Χ | Μ |
|---|---|---|---|---|---|
| Ι | Πεντε | Δεκα | Εκατον | Χιλιοι | Μύριοι |
| 1 | 5 | 10 | 100 | 1000 | 10000 |
Similares son el etrusco y el romano IVXLCDM. Los signos
romanos
no estaban relacionados en origen con el alfabeto (T. Mommsen, 1840) pero se forzaron a este por semejanza
gráfica siendo sin embargo los únicos acrófonos atribuibles C (centvm) y M (mille). Tanto uno como otro
tienen
un rasgo claramente anómalo: la sustracción en subsecuencias crecientes:
- suma si A>B:
MX = 1000 + 10 = 1010 - resta si A<B:
XM = 1000 - 10 = 990
tercera categoría
Es muy difícil sacar conclusiones de este grupo sin una muestra amplia o si se desconoce la secuencia
alfabética
en la que se basa puesto que no suelen repetir ninguna cifra en cada número. Existen muchos signos pues
existen
signos específicos para la combinación unidad·potencia 10, 20, 30... 100, 200, 300.


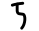 = 888
= 888
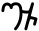

 = 555
= 555
En el brahmi sí se observa repetición, ya que no existe un signo específico para 600, 700, 800 y 900 y deben
componerse a partir de 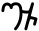 500.
500.
En otros sistemas de numeración las cifras se corresponden con letras de un alfabeto. Este vínculo facilita el arte esotérico de la numerología.
Los numerales griegos aparecen hacia el s. V AEC. Usan el antiguo alfabeto iónico y no llegarían al número 900 con el alfabeto estándar. Fueron adaptados al hebreo al final del s. II AEC y a otros como el árabe, geʽez, armenio, georgiano, glagolitico, o cirílico.
| Α | Β | Γ | Δ | Ε | 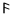 |
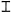
|
Η | Θ |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Ι | Κ | Λ | Μ | Ν | Ξ | Ο | Π |  |
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 |
| Ρ | Σ | Τ | Υ | Φ | Χ | Ψ | Ω | 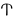 |
| 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 |
Hubo propuestas por parte de astrónomos y matemáticos para extender este sistema y poder representar
magnitudes
mayores utilizando la quinta potencia de la base B⁵ = 10⁵ = 10000. Como quiera que no existen
signos específicos para 1000, 2000, ..., 9000, obsérvese el uso de la unidad con valor doble
E=5000=5
- mediante principios multiplicativos como M = 3·10000 o M = 534·10000 = 5,340.000. Hallando por ejemplo:
'ZPOEM'EΩOE = 71,755,875 en Aristarco de Samos (310–230 AEC)
ΔΤΟΒ'Η

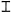 = 4372 · 10000 + 8097 = 43728097 en Diofanto de Alejandría (s. III AEC)
= 4372 · 10000 + 8097 = 43728097 en Diofanto de Alejandría (s. III AEC)
- Apolonio de Perga extendió el sistema con potencias M = 10000, M = 10000², M = 10000³, ...
M 'EΩOEχαι M 'ZPOEχαιΣΞΘ = 587,571,750,269, donde χαι significa 'más'
En hebreo (léase de derecha a izquierda) se añadían dos puntos sobre el signo para indicar su multiplicación por mil o bien se ordenaban crecientemente.
הם = םהֿ = 5060
65 = םה
A veces el sistema de potencias no está completamente especificado y en tales casos se resuelve por adición:
- En el sistema hebreo no existen signos para
500, 600, 700, 800 y 900, pero700 = 400 + 300 - En los numerales Brahmi. Puede observarse una cierta composición que sigue principios multiplicativos en las centenas y millares:

cuarta categoría
八百八十八=888
Consideremos el chino:
- ¿es un sistema aditivo? en el aditivo se agrupan y suceden los signos de igual valor, por ejemplo el
ático
𐅅ΗΗΗ𐅄ΔΔΔΠΙΙΙtiene un patrónaBBBcDDDeFFF. Pero aquí observamos un patrónAbAcA: la interposición de otros elementos entre signos iguales, lo cual implica que adquieren diferente valor por su contexto o posición. no, entonces - ¿es un sistema multiplicativo? en este caso habrá que distinguir unidades y potencias
一十二萬三十=120030
Reflexionando sobre este ejemplo, no es difícil asumir que ciertas cifras conservan el diseño de su etapa
aditiva
一=1, 二=2 y 三=3. Pareciera que 十=4 pero seamos prudentes:
por
ahora tenemos 1十2萬3十=120030. Asumimos base decimal; si observamos, 十 se interpone entre 1 y 2
por
lo que solo puede ser una potencia y como 3十=30 entonces 十=10 y consecuentemente
萬=10000.
Lo que caracteriza a esta categoría son los principios multiplicativos y tiene como paradigma a la numeración china tradicional. En esta observamos que existen cifras para las potencias y específicas para todas las unidades (números inferiores a la base):
- unidades: 1-9
一二三四五六七八九 - potencias: 10 100 1000 10000 10⁸ 10¹⁶ 10³²
十百千万億兆京
el orden creciente o decreciente implica diferentes operaciones aritméticas:
- adición si A>B
十一 = 10 + 1 = 11 - multiplicación si A<B
一十 = 1 * 10 = 10
Existen otros sistemas no paradigmáticos, con rasgos mixtos, como los que existieron en el sur de Arabia (sabeano, minaeano, ...).

En apariencia estamos ante un sistema similar al ático: aditivo por la repetición y agrupación de signos, base 10 y sub-base 5, aquí parcialmente acrofónico en 4 de sus 6 signos (otro, el 1, es como estamos acostumbrados, una línea vertical)
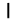 |
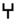 |
 |
 |
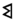 |
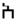 |
|---|---|---|---|---|---|
| /x/ | /ʕ/ | /m/ | /ʔ/ | ||
| /xamsat/ | /ʕasarat/ | /miʔat/ | /ʔalf/ | ||
| 1 | 5 | 10 | 50 | 100 | 1000 |
Parecido hasta que topamos con esto:
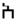
Hay un evidente principio multiplicativo. Pareciera, como en chino, que si una subsecuencia es decreciente
hay
adición, si es creciente multiplicación. Sin embargo, algo no cuadra ¿cómo se representa el número
280000?
Lo anómalo es que el signo creciente, en este caso 
quinta categoría
८८८=888
consideremos el caso del hindú
- ¿es un sistema aditivo? si así fuera ८८८ implicaría un valor
८=888/3=296pero como quiera que 296 no es la potencia de ninguna base más pequeña296=2·2·2·37, un número tan grande como 296 debería ser la base. Con esta base la igualdad de la segunda expresión१०००=1000sería imposible. Si el caso fuera otro, por ejemplo, la sucesión de 3 elementos tales que###=867⟶#/3=289y como289=17²la base sería 17. No, entonces: - ¿es un sistema multiplicativo? no porque descartado el aditivo deberían interponerse otros signos que
representen las potencias de la base. Es el caso de las potencias
百=100o十=10en el chino八百八十八donde八=8. - Concluimos que es un sistema posicional y al saberlo se deduce a simple vista que su base es 10,
bastando
con comparar el patrón de cifras
AAAen८८८=888con otro sistema decimal como el nuestro.

A diferencia del chino, en el sistema posicional la potencia de la base está implicita .
Esto
exige la creación de la posición vacante, origen del 0, cuyo estatus evolucionó hasta ser considerado un
número
más. Esto permite que una sucesión de cifras iguales como el hindú ८८८ equivalga implícitamente a
8·10² + 8·10¹ + 8·10⁰ = 800 + 80 + 8
 = 327
= 327
En el caso de la numeración con varillas 籌, diferente del sistema tradicional, podemos observar un diseño
aditivo
de las cifras, con 3 constituido con 3 líneas y análogamente la cifra 2. En el último segmento el valor de
la
línea horizontal es de 5=7-2. La segmentación no es fácil por la yuxtaposición y similitud de
los
signos por lo que se diseña una alternancia en la orientación: el segundo segmento 2 orienta
sus
líneas horizontalmente.
Es un sistema posicional que surge en el s. V AEC. La posición vacía se representaba con un espacio dando lugar a potenciales ambigüedades hasta que se adoptó por influencia del sistema numeral hindú un signo específico.
El caso maya y babilónico es más difícil de deducir por ser sus bases diferentes de 10 pero son sistemas posicionales. ¿cuáles son sus bases?
 = 59 o 3540
= 59 o 3540

Si observamos el babilónico y contamos el número de rasgos, en este caso marcas de cuña, veremos que cada cifra tiene un diseño aditivo no obstante distinto para unidades y decenas. Se parece a un sistema aditivo y decimal como el ático.
La duda la genera que los ejemplos también equivalgan a 3540 y 60 respectivamente. La relación existente es
3540=59·60+0 y 60=1·60+0 por lo que estamos ante el primer sistema de numeración
(2000
AEC) de base 60 y posicional en el cual la posición vacía no se representa (realmente sí se marca dejando un
espacio vacío pero si se ubica al final del número es ambiguo)
La elección de la base 60 tiene ventajas en el cálculo fraccionario, ya que es el número más pequeño que es
divisible por 1, 2, 3, 4, 5, 6 y 10 entre otros mientras que este intervalo la base 10 sólo lo
es
por 1, 2, 5 y 10 . Pervive en la geometría y en la medida del tiempo dos ámbitos muy asociados
a la
astronomía.
 = 42
= 42
2 2 = 42, lo que permite concluir una
base
20 puesto que:
2·B¹ + 2·B⁰ = 42 ⟶ B + 1 = 21 ⟶ B = 20;
No obstante el maya presenta una irregularidad en la segunda potencia de la base,
B²=18·20=180 y
no
B²=20·20=400 como se esperaba.
El babilónico y maya poseen sub-bases gráficas deducibles 10 y 5 respectivamente. Esto puede suscitarnos la pregunta ¿cómo se determinan las sub-bases más convenientes de una base? pues se elige un divisor cercano a la raíz cuadrada de la base, así:
- de 60 la raíz es ~7.7 y sus divisores son
1, 2, 3, 4, 5, 6, 10, 12, 15, 30 y 60. Por lo que elegiríamos uno del par divisor 6·10. - de 20 la raíz es ~4.5 y sus divisores son
1, 2, 4, 5, 10 y 20. Por lo que elegiríamos uno del par divisor 4·5.
Parametrización
| ¿cuántas potencias de la base hay? | ¿cuántas unidades tiene? | ¿qué operaciones aritméticas involucran la combinación de las cifras? | |
|---|---|---|---|
| mínimas | ninguna si estamos ante un sistema posicional (que implica la existencia del 0) | una en un sistema no posicional y dos en un sistema posicional (binario, 0 y 1) | adición |
| máximas | ilimitadas | tantas como la base en un sistema posicional (base 10: 0 1 2 3 4 5 6 7 8 9) y una menos en uno no posicional (sin el 0) | dos: adición y por otro lado multiplicación |
| casos singulares | potencias híbridas (10, 20, 30... 200, 300...) | sub-bases de apoyo gráfico (5 en base 10 y 20, 10 en base 60) irregularidades (secuencia incompleta: 1, 2, 3, 4, 10...) | sustracción en vez de multiplicación. En el caso del sistema posicional hay una exponenciación implícita de la base. |
* potencias híbridas: con signos específicos adicionales para decenas 20 30... y/o
centenas
200 300...
Podemos observar que en la mayor parte de las culturas, el signo para 1 es una línea. Tal diseño se observa también en las marcas de los huesos prehistóricos
Conclusión y categorías
Para una clasificación más pormenorizada lea el capítulo 23 del libro 'Histoire universelle des chiffres' de Georges Ifrah.
¿cómo obtiene una cifra como '3' su valor
300
en un número como 1315?
| valor | signos numéricos | origen | |
|---|---|---|---|
| A. la cifra | 1 10 100 1000... | egipcio 3000 AEC | fase aditiva. sólo existen las potencias de la base B⁰...B^n y no hay bases auxiliares gráficas |
| 1 5 10 50 100... | babilónico 2000 AEC | con sub-bases gráficas | |
| 123456789 10 20 30... 100 200 300... | griego, s. VII AEC | alfabético, con multitud de signos específicos para la combinación unidad·potencia | |
| B. cifra y contexto | 123456789 10 100 1000 10000 | multiplicativo, con diversas unidades y potencias | |
| C. cifra y posición | 0 123456789 | hindú s. V | posicional: bastan tantas cifras como la base. Exige el cero. |
A. cifra: en las tres primeras categorías la cifra determina el valor: basta con sumar todas las cifras para determinar el número, por lo que su orden es irrelevante a pesar de existir convenciones sobre su orden y agrupación (se exceptúa la numeración romana).
B. cifra y contexto: incorpora procedimientos multiplicativos y el valor lo determina la cifra y el contexto. Por ejemplo, en una subsecuencia, el orden creciente o decreciente implica diferentes operaciones aritméticas:
- suma si A>B:
mil diez = 1000 + 10 - multiplicación si A<B:
diez mil = 10 * 1000
Este principio multiplicativo se corresponde con un principio que ya existía en la expresión oral de la mayoría de las lenguas (Georges Ifrah, 1994).
Existen cifras para las potencias de la base y específicas para las unidades (números inferiores a la base).
C. cifra y posición: en el sistema posicional la cifra '3' puede
valer
3, 30 o 300 según su ubicación en los números 13, 131 o 311.
La notación explicita los coeficientes mientras las potencias están implícitas. En muchos sistemas no posicionales con principios multiplicativos se han hallado muestras abreviadas en las que se prescinde de las potencias, sin embargo no se ha completado el último requisito del sistema posicional: inventar un signo 0 para la posición vacante. Es el caso del sinhala:
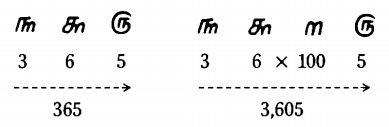
La sencillez y potencia del sistema no debe engañarnos: concebir este sistema exigió milenios y fue ignorado por civilizaciones avanzadas como la egipcia y la griega.
El sistema hindú perfecciona el sistema posicional, pero no fue el primero. Antes de este otras tres culturas lo idearon de una manera imperfecta:
- en el 2000 AEC, los babilonios
- poco antes del comienzo de nuestra era, los chinos
- entre el s. IV y IX, los mayas
Eran imperfectos en tres aspectos:
- diseño de las unidades: a pesar de poseer bases
60, 10 y 20el diseño de las unidades no era distintivo ni fácilmente percibible ya que se basaba en la adición de solamente dos rasgos gráficos: líneas de diferente orientación o bien punto y línea:
Este carácter ideográfico que sigue los principios de adición es reconocible en la mayoría de los
sistemas de
numeración en las primeras cuatro cifras como en १२३ / ١٢ ٣ / 123 o en el chino
一二三 pero también en 五=5. Para números superiores se impone el principio psicológico de que
es
difícil percibir a la vez más de cuatro elementos (Georges Ifrah, 1994), motivando otros diseños.
-
bases: la base maya no era sistemática ya que
B²=18·20y no como se esperaB²=20²=400. Esto supuso un perjuicio importante para su aritmética. -
el cero:
- su primera representación fue en el s. IV en el manuscrito Bakhshali. En la numeración indo/árabe se representa de manera mínima como un punto: por ejemplo en el signo árabe (٠)
- no fue desarrollado por la cultura china, que lo importó de los numerales hindús
- en la numeración maya se representa como
- en el sistema babilónico se expresaba mediante un espacio vacío dando lugar a inevitables
ambigüedades (posiciones vacías sucesivas
00..., o finales...0) como en2 y 120 (2×60),3 y 180 (3×60),4 y 240 (4×60). Posteriormente, en el s. IV AEC, aparece el cero en posición media:
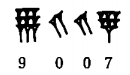
Su representación no implica sin embargo su inmediato estatus como un número más similar a
1, 2...9
¿cuál es su etimología? en indio es 'sunya' que significa vacío y en chino 零:
From Middle Chinese零 (leng) with an original meaning of a small rainfall. The character was later repurposed in 1248 by mathematician Li Ye to mean zero, extending from its a little bit (of rain) meaning to indicate *a bit more remaining
Este sistema posicional capacita a los signos para las operaciones aritméticas lo cual contrasta con los anteriores sistemas que son notaciones abreviadas.
Bibliografía
Ifrah, G. (2000). The universal history of numbers : From prehistory to the invention of the computer. New York etc: John Wiley.
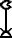


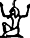
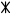

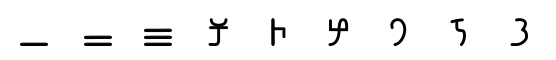

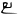

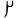
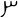


 (1
y
10; 0 vacante)
(1
y
10; 0 vacante)
